在瞬息万变的金融市场中，期权作为一种重要的金融衍生品，为投资者提供了对冲风险、放大收益的工具。期权的价值并非一成不变，其价格受到标的资产价格、行权价格、到期时间、波动率和无风险利率等多种因素的影响。准确地对期权进行定价，是投资者和金融机构进行风险管理和投资决策的关键。在众多期权定价模型中，二叉树模型以其直观易懂、灵活性强等特点，成为了金融工程领域中一个基础且广泛应用的工具。

二叉树模型（Binomial Tree Model），又称二项式期权定价模型，由考克斯、罗斯和鲁宾斯坦（Cox, Ross, and Rubinstein, CRR）于1979年提出。它通过将标的资产价格在期权有效期内可能发生的变动离散化，构建一个树状结构来模拟价格路径，进而倒推出期权的当前合理价格。该模型的核心思想是基于“无套利原理”，即在有效市场中，不存在无风险套利机会。通过构建一个能够精确复制期权未来收益的投资组合，即可确定期权的当前价值。

期权基础与二叉树模型概述

在深入探讨二叉树模型之前，我们有必要简要回顾期权的基本概念。期权是一种“权利而非义务”的合约，赋予其持有者在未来特定时间（或时间段内），以特定价格（行权价格）买入或卖出标的资产的权利。根据权利的不同，期权可分为看涨期权（Call Option）和看跌期权（Put Option）。看涨期权赋予购买者以行权价格买入标的资产的权利，而看跌期权则赋予其卖出标的资产的权利。根据行权时间的不同，期权又可分为欧式期权（只能在到期日行权）和美式期权（可在到期日或到期日之前的任何时间行权）。

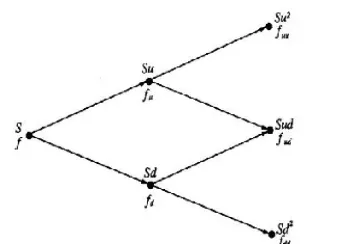
二叉树模型正是为了解决期权定价问题而生。它将期权的整个生命周期划分为若干个离散的时间步长。在每个时间步长结束时，模型假设标的资产（如股票）的价格只有两种可能的变化：上涨（Up）或下跌（Down）。这种“一分为二”的简单假设构成了二叉树的每一个分支，从而在整个期权有效期内形成一个由无数个节点组成的树状结构。通过这种方式，二叉树模型能够模拟标的资产价格在未来所有可能的路径，并在每个节点处计算期权的价值。

二叉树模型的核心在于“无套利”定价原则。它通过构建一个由标的资产和无风险债券组成的“复制组合”，使得该组合在未来任何状态下的收益都与期权的收益完全相同。根据无套利原则，这个复制组合的当前价值就应该等于期权的当前价值。这种方法避免了对未来市场方向的预测，而是专注于构建一个风险中性的定价框架。

单期二叉树模型详解

理解二叉树模型的最佳起点是单期二叉树模型，即假设期权有效期内只有一个时间步长。让我们考虑一个简单的例子：

假设当前股票价格为$S_0$，在未来的一个时间步长后，股票价格可能上涨到$S_u$（上涨因子为$u$），也可能下跌到$S_d$（下跌因子为$d$）。同时，我们假设市场存在一个无风险利率$r$。

对于一个欧式看涨期权，其行权价格为$K$，到期日为$T$（即一个时间步长）。在期权到期时，如果股票价格上涨到$S_u$，看涨期权的价值将是$C_u = \max(0, S_u - K)$；如果股票价格下跌到$S_d$，看涨期权的价值将是$C_d = \max(0, S_d - K)$。

为了计算期权在当前时刻$C_0$的价值，我们构建一个由$\Delta$份股票和借入$B$元无风险债券组成的复制组合。这个组合在未来时刻的价值应该与期权价值相等：

如果股票价格上涨：$\Delta \cdot S_u - B \cdot (1+r) = C_u$

如果股票价格下跌：$\Delta \cdot S_d - B \cdot (1+r) = C_d$

通过解这两个联立方程，我们可以得到：

$\Delta = \frac{C_u - C_d}{S_u - S_d}$（表示每份期权需要复制的股票数量，也称为对冲比率）

我们可以将$\Delta$代回任意一个方程，解出$B